All of the text and diagram from the “Essentials of Music Theory” can also be downloaded as an ebook, in PDF format. Click here, or on the book image below, to get it.
PART ONE
Keys, Scales, and Chords
In Part 1 of the Essentials of Music Theory for the Clawhammer Banjoist, it’s all about keys, scales, and chords. We’ll be building the fundamentals first, and then learning how to apply them to specific situations on the banjo.
Begin by watching the video of Part 1 below. You can then review the concepts presented in the video with the subsequent transcript (plus diagrams) of the video, or proceed on to the Part 2 video.
The very concept of “music theory” is associated with a lot of baggage. Just the word “theory” is enough to cause some folks to run for the hills.
Like the subject of math or science, many folks have talked themselves out of understanding before they even take a real shot at it, in so doing depriving themselves of the benefits that come with that understanding.
But there’s a couple of things I want you to keep in mind:
1) It’s probably not nearly as complicated as you think.
2) I’ll only be covering the parts that are USEFUL (and that’s not a contradiction in terms!). We won’t be covering the bits of theory that are purely of academic interest. Too many times music theory is taught with little or no regard to what parts are useful, or how to actually MAKE it useful.
We’ve covered a bit of theory in some of the other modules, so if you’ve been through those, some of this may be a review. This will also be true if you’ve had any prior exposure to the subject.
But I think reviewing these concepts is almost always a good thing. Repeat anything enough times, and what may seem inscrutable and foreign at first will become simple and familiar.
My primary objective here is to dump all the useful banjo-relevant bits of theory out from my brain and into yours. So let’s get started.
What Is Theory?
All music, from classical to jazz to punk to old time is just regular vibrations of air molecules put together in ways we find appealing. We find those sounds appealing because there’s an order in the way they’re put together. One definition for music is “organized sound”.
Disorganized sound, on the other hand, we call noise.
Every piece of music that we play is usually just a combination of 3 elements: melody, harmony, and rhythm. And there are rules that govern how these elements are put together.
Music theory simply explains the logic behind those rules. That’s it. You can absolutely make great music without ever knowing – in a formalized sense – what those rules are. But, understanding a bit of that logic can actually make your life easier as a musician.
The bits of theory that aren’t practical, that are more about intellectual curiosity and truth seeking, are primarily the domain of academicians (though feel free to dig further on your own into the esoterica should you so desire!).
Also, you may think that to understand theory you need learn a bunch of symbols and Latin sounding names. Not really. You just need this if you want to write or talk about music theory, as these labels help create a common language.
But to understand it, you just need to understand the concepts, which is what we’ll cover here. Symbols and other arcana will only be discussed on a “need to know” basis.
Lastly, it’s not important that you memorize the material here. What’s important is that you understand the concepts.
And if anything is still unclear after going through this, please don’t hesitate to get in touch with me. Strangely enough, I actually enjoy talking about this stuff!
Situational Theory
To make this as practical as possible, I’m going to center this discussion of theory primarily around the specific situations where it can be useful for a banjo player.
But before we get to those situations, we need to build a bit of a foundation by talking about scales, keys, and chords.
The Scale
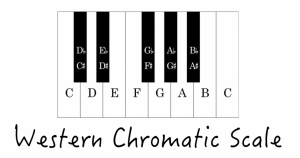
I’m sure you’ve seen a piano keyboard before. It looks like this:
These are essentially all the notes in the “Western Chromatic Scale”, so this is the set of possibilites you’re choosing from when you’re playing music on the banjo (though if you’re playing a FRETLESS instrument, you can choose to play sounds in between these scale notes).
Each note in the scale refers to a string that vibrates at a specific rate. We’ve decided to call a string that vibrates at 440 vibrations per second, for example, an A. We’ve decided to call a string that vibrates at 523 vibrations per second a C. What we choose to call them is arbitrary.
There are 12 possible notes in all (A, Bb, B, C, C#, D, D#, E, F, F#, G, G#), as these notes repeat themselves several times over on the keyboard.
Now, if we were to play a song that indiscriminately used all the notes on the keyboard, it would sound horrible. Neither you nor I would enjoy it very much.
Why not?
Because our ears (or rather, our brains) expect music to be played in a particular key. Years of listening to music has trained our brains to do so. You actually have a sophisticated internal sense of music theory, which you’ve been learning (thanks to the magic of subconscious pattern recognition) all of your life.
Music that fits within those rules you find pleasing. Music that doesn’t you find unpleasant (unless you’ve cultivated unusual tastes).
So, once again, your brain expects a song to be played in a particular key. And every key has its own particular set of notes. It’s those specific notes that determines what key you’re playing in.
How many notes out of the possible 12? 7.
These 7 notes are the scale in that key. You know, the “do-re-mi-fa-so-la-ti-do” (since the “do” is the same note, you don’t count it twice).
How exactly do you figure out the allowable notes in a particular key? By following the rules of scale creation.
The Rules of Scale Creation
To create any scale, all we need to do is begin with the first note (an A scale begins with an A, a B scale begins on a B, and so on…), and then apply the rules of scale creation until we have all 7 notes.
To illustrate, let’s return to the piano keyboard again:
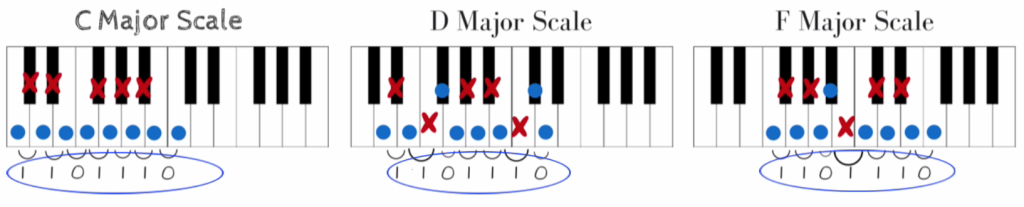
So let’s create our C major scale. Now, those of you who have any piano background likely know that the notes of the C major scale are simply the white keys of the piano. If we start with C, then play the white keys until we get to the next C, we get the “do-re-mi….” scale. Here’s what that sounds like.
Let’s now try creating a D major scale. But let’s not worry about the notes just yet, let’s just try to play the “do-re-mi” part again using only our ears as a guide. Again, we’ll start on a D, and play “do-re-mi”. Here’s what that sounds like.
Here, we can’t just stick to the white keys. In order to make our scale sound right, we had to include two of the black keys, in this case the F# (the black key above the F) and the C# (the black key above the C).
Now, let’s try playing the F major scale, again entirely by ear. Here’s what that sounds like: [f major scale]. And here’s what it looks like on the piano. Again, we had to include one of the black keys to make it sound right.
Minding the Gaps
With this little exercise, we’ve illustrated that each key has its own distinct notes of its scale. Let’s now look at these examples to see if there’s a pattern to it – a pattern that will reveal the rule of scale creation.
Here’s what each of those scales look like on the keyboard, with the notes of each scale marked in blue.
To find the pattern, what we need to focus in on are the spaces, or the gaps, in the keyboard between the notes. Let’s look at these 3 scales again, this time noting how many spaces are between each note with an X.
Notice something? The pattern of gaps between the notes (denoted by the red “X”) of the scale is the same in every scale:
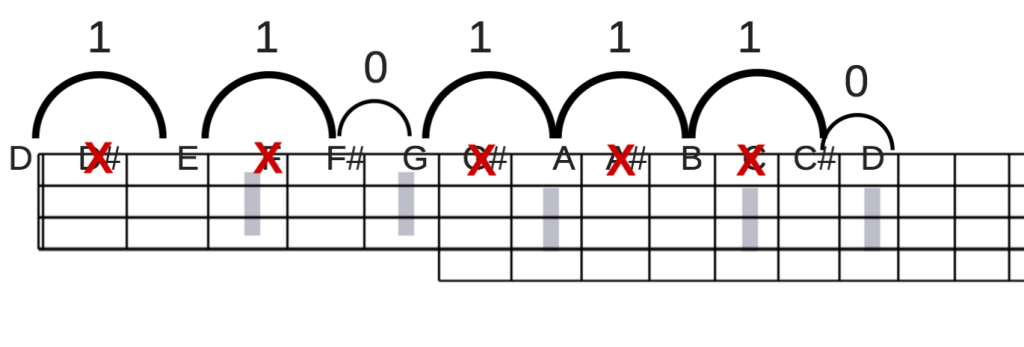
In other words, to create the major scale for any key, we play the first (also known as the “root”) note, skip one, play the next, skip one, play the next, play the next, skip one, play the next, skip one, play the next, skip one, play the next, and play the next (which gets us back to our original note, just an octave higher).
We can also map this exact pattern to the banjo fretboard, as the frets on the banjo correspond to the keys of the piano. Play a D scale on the 1st string and we have:
Again, here you can apply the rule, or just use your ear. Just start with any note on the banjo fretboard, and play the “do-re-mi” scale.
Now, for much of banjo playing, especially clawhammer style, memorizing scales isn’t that useful, and so the return on investment is low. Your practice time is typically better spent elsewhere.
However, understanding this bit about how scales are constructed will help you understand the relationships between keys, and understand how chords are constructed, which are useful things to know.
Take Home Points About Scales
- A scale is the set of notes that define a particular key. If you’re playing a song in a given key, these are the notes you’ll be using (with occasional exceptions).
- To find the notes of a scale by ear, simply start with the first (or “root”) and pick out the “do-re-mi-fa-so-la-ti-do” series.
- You can also find the notes of the scale by applying the rule of scale creation.
Banjo Tunings and Keys
One of the more unique features of the banjo, as I’ve mentioned before, is that it’s typically played in “open” tunings, as the style in which a banjo is played sounds best with these types of tunings. This means the strings are tuned to a particular chord.
This also means that the tuning is intended to be played in a specific key.
This is unlike the guitar, where the standard tuning is not “open” (if you strum the open strings of a guitar in its standard tuning, it’ll sound quite terrible), which allows the guitarist to play in any key out of this tuning.
As you may know, the two tunings I spend the most time in are standard G and double C.
Standard G tuning, gDGBD, is used for songs in the key of G.
Double C tuning, gCGCD, is used for songs in the key of C.
If we wish to play songs in other keys but still use the same tuning relationship between the strings as these tunings (and not have to alter the way we play the tune in any way), we must use a capo, which we’ll discuss more about in a bit.
The Rule Of Chord Creation
Now that we understand the rule of scale creation, we can also understand the rule of chord creation.
But first, let’s be sure that we all understand exactly the whole point of chords. I played music for years, and knew how to play chords, before I really understood the whole point of them in the first place. And that’s a really good place to start.
As I said earlier, all music has 3 main elements: melody, harmony, and rhythm.
The melody is just the sequence of notes in the tune.
The harmonies are the notes that sound good when played alongside the melody notes. And what harmony notes sound good played alongside the melody changes as the song goes on.
The chord progression for a song tells you what those harmony notes are at any point in time. So, if you’re looking to provide harmony for a melody (as a backup musician, etc.), then knowing the chord progression is a big shortcut. It spells out exactly what notes will sound good played alongside the melody notes at any point in time during the tune. That’s it!
And a chord is just 3 or more notes that, when played together, sound pleasing (2 notes played together that sound pleasing is called a partial chord)
Now, as we did with the scales, let’s look at a few chords and see if we can extract the rule of chord creation.
Let’s take the example of the C, F, and G major chords. Just like every key has a set of notes that sound good (the scale), every key also has a set of chords, and these chords are built from the notes of the scale. The C, F, and G major chords are all chords in the key of C.
The C major chord consists of the notes C, E, and G. If you play these 3 notes at the same time, you’ll find it sounds quite nice. The F major chord consists of the notes F, A, and C. And the G major chord consists of the notes G, B, and D.
And then let’s look at the notes of the C major scale again:
C D E F G A B C
As you can see, all of the notes in the C, F, and G major chords are contained within the C major scale, since these are all acceptable chords in the key of C. So here are the notes of those chords again, now in the color blue, inside the scale sequence:
C major chord: C D E F G A B C
F major chord: C D E F G A B C
G major chord: C D E F G A B C D
Do you notice the rule of chord creation here? I bet you did. To create these chords, all we did was take the root note of the chord (so a C chord would have C as its root note), skip one note in the scale, play the next note, skip another note in the scale, and play the next note. Now we’ve found our 3 note chord.
And, just as we only really have 7 primary notes to choose from when playing in any particular key, we also only have 7 primary chords to choose from when playing in any particular key.
How do we find out what those 7 chords are? Just start with the first note of the scale, apply the rule of chord creation to each note, and stop once you’ve completed the scale.
So, here are all of the chords in the key of C. Again, the notes of the chord are highlighted in blue.
Chord I: CEG (C D E F G A B C)
Chord ii: DFA (C D E F G A B C)
Chord iii: EGB (C D E F G A B C)
Chord IV: FAC (C D E F G A B C )
Chord V: GBD (C D E F G A B C D)
Chord vi: ACE (C D E F G A B C D E)
Chord vii: BDF (C D E F G A B C D E F)
So every key is going to have 7 primary chords that sound good. Which means, when trying to find the chord progression for any song, these are the 7 primary chords you can choose from (there are additional modifications that can be made to these chords to give them a slightly different sound, and how much you do this type of thing depends largely on the style of music you’re playing; regardless, these 7 chords will always be your starting point).
By convention, we use Roman numerals to refer to these chords, as follows: I, ii, iii, IV, V, vii, vi.
Why, you ask, are some chords represented as a capitalized number, and some as lower case? As it turns out, some of these chords (I, IV, and V) are major chords, some of these (ii, iii, and vii) are minor chords, and one chord is neither major or minor (vi). So, the major chords are designated by capital letters, the others a lower case.
Now, using this system, if someone tells you a song uses just the I, IV, and V chords in the chord progression, you can know what those chords will be regardless of what key you decide to play the song in. This is why the numbering system is so useful, because it’s a universal system for talking about a chord progression, irrespective of the particular key that you’re in.
If your song uses the I, IV, and V in the key of D, for example, and you decide to switch to playing it in the key of E, you’ll still be playing the I, IV, and V chords – in the key of E.
So we can use this understanding to our advantage. Now we know that every key has a set of chords that sound good in that key, and those chords are constructed from just the notes of the scale.
Playing Chords on the Banjo
Armed with the rules of chord construction, you can now find any chord you want on the banjo fretboard; however, where we find those chords will depend on the particular tuning we’re in.
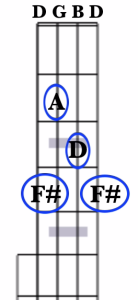
For example, let’s find the I, IV, and V chord in the key of G in standard G tuning. Those chords would be G major, C major, and D major.
To find the 3 notes of the G Major chord, we need to locate a G, B, and a D on our banjo. Conveniently, these can all be found on the open strings of the banjo in this tuning. Just strum the banjo in this tuning, and you’re playing a G Major chord. The notes you’re playing are DGBD.
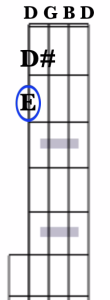
To find the notes of the C Major chord, we need to locate a C, E, and G note. Our open 4th string is tuned to a D, so the closest chord note is the E note, located at two half steps away at the 2nd fret.
Our open 3rd string is tuned to a G, so we can just leave it alone since it’s already a chord note. Our open 2nd string is tuned to a B, so the closest chord note is the C note, just one half step away at the 1st fret.
Lastly, our open 1st is a D, like the 4th string, so once again we’ll grab an E note at the 2nd string.
So now we’re fingering a C chord, EGCE (strings 1-4).
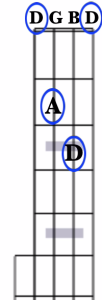
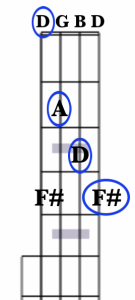
To find the notes of the D major chord, we need to find the notes D, F#, and A. Our open 4th string is already tuned to a D. The closest chord tone to our open 3rd string, which is tuned to a G, is the A note, which we can find at the 2nd fret. The closest chord tone to our open 2nd string is the D note, found at the 3rd fret. Now, if we were to just finger these notes and leave the 4th and 1st strings open, we’d have DADD.
You’ll notice that we’re missing the 2nd note, the F#, of our full chord.
What we have now is known as a partial chord, as it contains only two notes of the chord. And while this isn’t the fully formed major chord, the partial D chord will “work” any time a D chord is called for in a tune, since there are no “wrong” notes there (I like the way this chord sounds, and do use it quite a bit in my own playing!).
However, if we wish to play the full D chord, then we need to find that F#. The most convenient location to find it is at the 4th fret on both the 1st and 4th string. So, a fully fingered D chord looks like this:
And we’re playing the notes F#ADF#. Another alternative here, which will also give you all 3 notes of the full D Major chord, is to leave the 4th string open, like this:
Now we’re playing the notes DADF#.
As you can see, knowing a bit of music theory, and how chords are constructed, gives you several options you might not have realized were available to you.
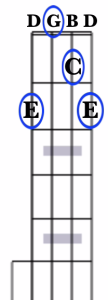
Now, these are far from the only places on the fretboard where you can play these chords. Any time you’re playing the notes C, E, and G together, for example, you’re playing a C chord. And there are multiple places on the fretboard where you can do so:
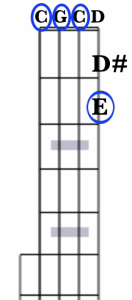
For the sake of illustration, let’s find a C major chord in “double C” tuning (gCGCD). You’ll note that the open 2nd through 5th strings are all Gs and Cs. All that’s left is for us to find our E note.
Since that D note that the open 1st string is tuned to isn’t part of our chord, let’s find it there. And since an E note is 2 half steps up from a D, we’ll find it at the 2nd fret.
So, in double C tuning, all we must do to finger a C major chord is finger the 1st string at the 2nd fret. Strum the banjo, and you’ve got the C major chord.
In general, however, double C tuning is not particularly well suited to playing chords, especially chords in keys other than C. It tends to be most appropriate for the old-time repertoire of music, as these tunes weren’t created in the “chord first” manner that characterizes many other styles of music. This is why if we wish to play a tune in another key but still use the same tuning relationship of the strings, it’s best to use a capo instead.